Теорема синусів — це важливе математичне правило, яке використовується у тригонометрії для розв’язання трикутників. Вона дуже корисна, особливо коли ми працюємо з не прямокутними трикутниками. Зрозуміти її не так вже й складно, якщо пояснити все простими словами.
Що таке теорема синусів?
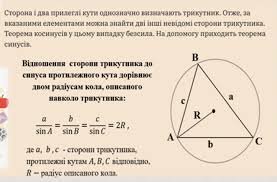
Теорема синусів допомагає знайти невідомі сторони або кути будь-якого трикутника. Вона говорить про те, що відношення сторони до синуса протилежного кута в усіх трикутниках однакове.
Це виглядає так:
a / sin(α) = b / sin(β) = c / sin(γ)
Тут:
- a, b, c — сторони трикутника.
- α, β, γ — кути навпроти відповідних сторін.
Чому теорема синусів важлива?
Насправді, теорема синусів є дуже зручною. Завдяки ній можна знайти довжину сторони або величину кута, коли відомо хоча б три елементи трикутника. Наприклад, якщо ви знаєте дві сторони і один кут, можна знайти інший кут або сторону. Це значно спрощує задачу!
Як запам’ятати теорему синусів?
Щоб легко запам’ятати теорему синусів, можна подумати про баланс або справедливість. У будь-якому трикутнику «великий кут» має бути навпроти «великої сторони», і навпаки. Якщо ми поділимо сторону на синус кута навпроти, у всіх випадках отримаємо одне і те саме число.
Приклад задачі з використанням теореми синусів
Задача:
У трикутнику відомо:
- сторона a = 7 см,
- кут α = 45°,
- кут β = 60°.
Знайти сторону b.
Рішення:
Спочатку знайдемо третій кут:
γ = 180° – 45° – 60° = 75°
Тепер застосуємо теорему синусів:
7 / sin(45°) = b / sin(60°)
b = (7 × sin(60°)) / sin(45°)
Обчислимо за допомогою калькулятора:
- sin(45°) ≈ 0.7071
- sin(60°) ≈ 0.8660
b ≈ (7 × 0.8660) / 0.7071 ≈ 8.57 см
Отже, сторона b приблизно дорівнює 8.57 см.
Коли застосовується теорема синусів?
Є кілька ситуацій, коли теорема синусів особливо корисна:
- Коли відомі дві сторони і кут між ними.
- Коли відомі дві сторони і кут, який не між ними.
- Коли відомі один кут і дві сторони, які прилягають до цього кута.
У всіх цих випадках ми можемо скористатись теоремою синусів, щоб дізнатись інші елементи трикутника.
У чому різниця між теоремою синусів і теоремою косинусів?
Це важливе питання!
- Теорема синусів працює з відношеннями сторін і синусів кутів.
- Теорема косинусів дозволяє знайти сторону або кут, якщо є три елементи, але вона складніша у вигляді.
Отже, теорема синусів легша для використання, якщо відомі кути.
Поширені помилки при застосуванні теореми синусів
Навіть учні з гарними оцінками іноді помиляються. Ось кілька типових помилок:
- Не переводять кути у градуси або не використовують правильні значення синусів.
- Забувають знайти третій кут, коли він необхідний.
- Плутають, яка сторона відповідає якому куту.
Щоб уникнути помилок, завжди робіть підписану схему трикутника.
Практичне використання теореми синусів у житті
Можливо, ти не думав, але теорема синусівв часто використовується у реальному житті. Наприклад:
- У геодезії — для вимірювання відстаней на місцевості.
- У навігації — щоб обчислювати курси та напрямки.
- У архітектурі — для побудови складних конструкцій.
Навіть інженери в авіації користуються нею для побудови траєкторій польоту!
Як перевірити себе?
Після розв’язання задачі, завжди можна перевірити, чи правильно ви застосували теорему синусів. Просто обчисліть кожне відношення: a/sin(α), b/sin(β), c/sin(γ) — якщо вони однакові, то все правильно!
Теорема синусів у ЗНО та шкільних екзаменах

Теорема синусівв обов’язково зустрічається у темі «Тригонометрія» під час підготовки до ЗНО. Якщо ви хочете набрати високий бал, потрібно вміти розв’язувати задачі з теоремою синусів швидко та без помилок. Порада — практикуйтеся щодня, навіть по 15 хвилин.
Пояснення синуса простою мовою
Синус — це відношення. У прямокутному трикутнику синус кута — це відношення протилежного катета до гіпотенузи. Саме через це синуси кутів допомагають знайти пропорції в трикутниках.
Як вивчити формули без зубріння?
Є кілька хитрощів:
- Намалюй кольорову шпаргалку на стікері.
- Вчи формули у формі пісні або рими.
- Поясни правило комусь іншому — так ти запам’ятаєш краще!
Переваги вивчення теореми синусів
Знання теореми синусів відкриває двері до складніших тем у математиці. Також вона тренує логіку, уважність, і навіть трохи уяву, бо потрібно уявляти трикутники в голові.
Теорема синусів і комп’ютерна графіка
Несподівано, але теорема синусів корисна в комп’ютерній графіці. Розробники ігор або анімацій використовують її для розрахунку положень об’єктів, кутів огляду, освітлення та навіть траєкторій руху персонажів.
Читати далі: Теорема Піфагора – просте пояснення з прикладами для учнів
Часті запитання (FAQ)
Теорема синусів — це правило в тригонометрії, яке встановлює рівність між сторонами трикутника та синусами протилежних кутів.
Її застосовують для розв’язання будь-яких трикутників, особливо коли відомо два кути та одна сторона або дві сторони та кут.
Теорема синусів простіша та працює з кутами і сторонами, тоді як теорема косинусів більше підходить для задач зі сторонами без відомих кутів.
Так, можна, але у прямокутному трикутнику є простіші способи — наприклад, використання синусів і косинусів напряму через катети та гіпотенузу.
Вона розвиває математичне мислення, допомагає готуватись до ЗНО і потрібна у багатьох професіях: від інженерії до програмування.
Висновок
Теорема синусів — це не просто формула, а справжній ключ до розв’язання геометричних задач. Вона допомагає мислити логічно, вчить шукати зв’язки між величинами та відкриває двері у світ складної, але цікавої математики. Якщо ти ще її не вивчив — саме час це зробити!







